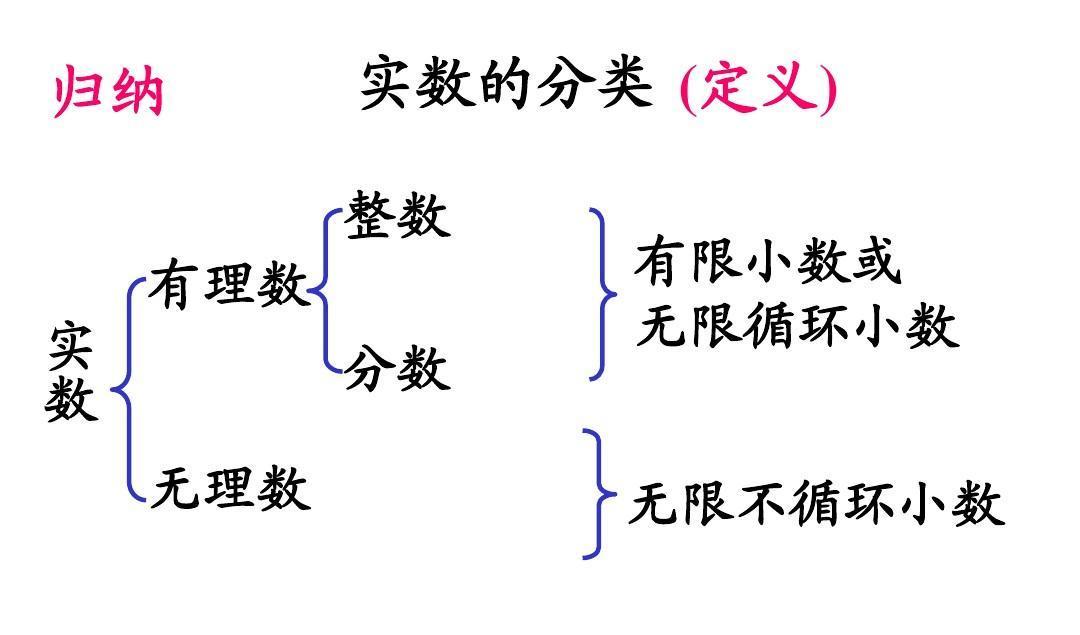
通俗地认为,通常包含所有有理数和无理数的集合就是实数集,通常用大写字母 R表示。
定义是由四组公理为基础的:
1.1.对于任意属于集合 R的元素 a、 b,可以定义它们的加法 a+ b,且 a+ b属于 R;
1.2.加法有恒元0,且 a+0=0+ a= a(从而存在相反数);
1.3.加法有交换律, a+ b= b+ a;
1.4.加法有结合律,( a+ b)+ c= a+( b+ c)。
2.1对于任意属于集合 R的元素 a、 b,可以定义它们的乘法 a· b,且 a· b属于 R;
2.2乘法有恒元1,且 a·1=1· a= a(从而除0外存在倒数);
2.3乘法有交换律, a· b= b· a;
2.4乘法有结合律,( a· b)· c= a·( b· c);
2.5乘法对加法有分配率,即 a·( b+ c)=( b+ c)· a= a· b+ a· c。
3.1∀ x、 y∈ R, x< y、 x= y、 x> y中有且只有一个成立;
3.2若 x< y,∀ z∈ R, x+ z< y+ z;
3.3若 x< y, z>0,则 x· z< y· z;
3.4传递性:若 x< y, y< z,则 x< z。
(1)任何一个非空有上界的集合(包含于 R)必有上确界。
(2)设 A、 B是两个包含于 R的集合,且对任何 x属于 A, y属于 B,都有 x< y,那么必存在 c属于 R,使得对任何 x 属于 A, y属于 B,都有 x< c< y。
符合以上四组公理的任何一个集合都叫做 实数集,实数集的元素称为 实数。