理想约束

定义

作用在质点上的力（包括约束反力）在任意虚位移δ r中所作的功，叫做虚功，如果作用在一力学体系上诸约束反力在任意虚位移

根据约束力作实功等于零，常见的光滑固定面约束、光滑铰链、无重刚杆、不可伸长的柔索、固定铰链支座、滚动支座、固定端等约束均为理想约束，现从虚功角度看，这些约束仍然为理想约束。另外，由于固定粗糙平面约束力对纯滚动刚体所做的实功与虚功均为零，也可认为粗糙平面对纯滚动的约束为理想约束。

几种常见情况

光滑接触面约束

光滑接触面约束的约束反力总两接触面上通过接触点的公法线方向，而质点的虚位移在接触面过接触点的切面上（如图1所示）。因此，约束反力在任何虚位移中的虚功恒等于零。

图1 光滑接触面约束

无重刚杆约束

图2所示为一无重刚性杆连接两质点，A、B两质点的约束反力

图2 无重刚杆约束

连接两刚体的光滑铰链约束

图3所示，刚体A、B由光滑铰链连接在一起。作用在销钉O上的约束反力

图3 连接两刚体的光滑铰链约束

不可伸长的绳索

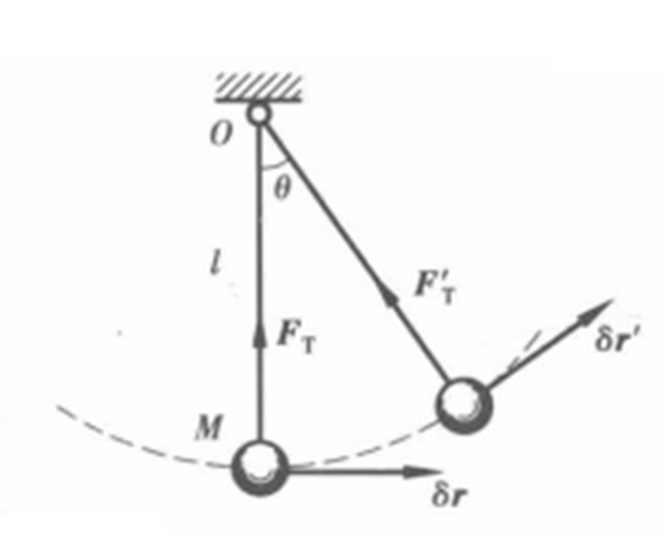
图4所示为一单摆，单摆由一端固定，另一端系住一质点M的不可伸长的绳索组成。设绳索不可伸长，小球在绳索的约束下，可在平面内摆动。将小球视为一个质点，如果在运动中，始终满足约束条件，绳索既不松弛也不蜷曲，小球在铅垂位置时，绳子给小球的约束力

图4 不可伸长的绳索

无滑动的滚动

如图5所示，圆轮在固定约束面上作无滑动的滚动，如果接触面足够刚性，可以略去滚动摩阻力偶，则当轮子作无滑动的滚动时，轮子与约束面的接触点是轮子作平面运动的瞬心C，可以将轮子的运动看做是绕瞬心C作瞬时转动，C点处的虚位移为零，约束轮子运动的法向力和摩擦力都通过C点，因此有：

图5 无滑动的滚动

研究意义

力学研究中，理想约束具有重要的意义，实例也非常多，如质点强制地沿固定光滑面的运动，质点强制地沿运动的或变形的光滑面的运动，圆球或圆盘沿完全粗糙的水平面作纯滚动，两刚体间理想光滑接触，两刚体间光滑铰接，等等。经典力学和现代力学的大多数理论研究都是基于该假设的．因此具有非常重要的意义。

同时该假设的工程实际应用也是完全可能的，且实际效果也非常成功。这是因为，第一，为描述自然现象和大多数技术过程，必然要做各种各样的假设，而理想约束这样的假设有足够的精确度。如复杂的机构系统可看成是刚体系统，其中刚体两两之间或刚性连接后铰链联结或以其表面相接触。第二，即便系统所受约束不是理想约束．我们也可以将其作为主动力来考虑，如摩擦力作虚功，可将其归为主动力范畴来考虑，由于未知量摩擦力的出现而缺少的方程由摩擦定律来补充。分析力学在处理约束问题上这一创造性的特点，具有重要的理论及实际意义。