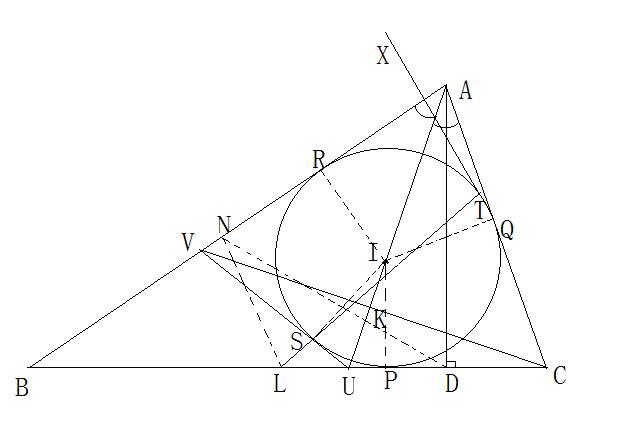
三角形的九点圆与其内切圆以及三个旁切圆相切。
设
的内心为I，九点圆的圆心为。三边中点分别为，内切圆与三边的切点分别是，三边上的垂足分别为。全局图
不妨设。假设
与相切于点，那么LT与相交，设另一个交点为。过点
作的切线，分别交和于，连接。又作两圆的公切线
，使其与边位于的同侧。由假设知
而
和都是的切线，且与弦所夹的圆弧相同，于是局部图1
因此则
这就是说，
共圆。而这等价于：
又
故有
另一方面，
是公共的切点，自然在上，因此
共圆，进而有局部图2
由已导出的共圆，得而
（这里用了
，以及直角三角形斜边上中线等于斜边的一半）所以，就得到
注意到
均与相切，于是有三式相加，即知
也即是说
三点共线。另外，
，这可由得到。（这说明，公切点
可如下得到：连接
，并延长交于点，过点
作的切线，切点为，交于，最后连接
，其延长线与的交点即是所谓的公切点。连接
，与交于点，则
是的中点。前面已得到：
而
即
然而
是的中位线于是
因之
故
由于以上推导均可逆转，因此我们只需证明：
。往证之这等价于：
与圆相切于是只需证：
局部图3
再注意到（是的中位线），即有又
是角平分线，于是于是又只需证：
即证：
这即是证：
四点共圆由于
（易得），所以
确实共圆。这就证明了
与内切。旁切圆的情形是类似的。
证毕
另略证：
(其中是垂心H的垂足三角形的内切圆半径，是三角形外接圆和内切圆半径)这就证明了九点圆与内切圆内切（九点圆半径为外接圆半径一半。是九点圆圆心，为内心）
金田明夫
贾科莫·普契尼
Caroline Lufkin
翁建宇
Ivanov
玛丽亚·凯莉
Delta值
两值期权
生育保险基金
skdj超买
卡尔多经济周期模型
慢速随机指标