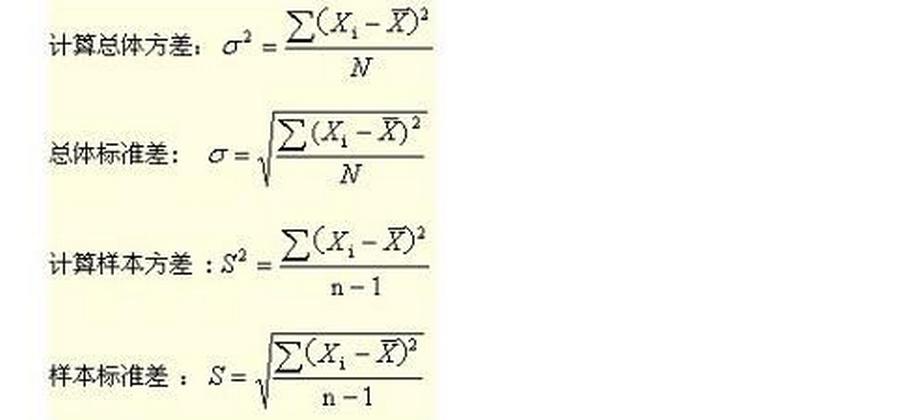
先求出总体各单位变量值与其算术平均数的离差的平方，然后再对此变量取平均数，就叫做样本方差。
在许多实际情况下，人口的真实差异事先是不知道的，必须以某种方式计算。当处理非常大的人口时，不可能对人口中的每个物体进行计数，因此必须对人口样本进行计算。样本方差也可以应用于从该分布的样本的连续分布的方差的估计。
我们从一个样本取n个值
，其中，并根据这个样本估计方差。直接取样本数据的方差给出平均偏差的平均值：这里，表示样本均值。由于 是随机选择的，所以 和 是随机变量。他们的预期值可以通过从群体中的大小为n的所有可能样本 的集合进行平均来评估。对于，有因此
给出了基于因子 的人口方差的估计值。被称为偏样本方差。纠正该偏差之后形成无偏样本方差：估计值可以简单地称为样本方差。同样的证明也适用于从连续概率分布中抽取的样本。例如，
个样本观测值值为则样本均值= ，样本方差 。样本方差是常用的统计量之一，是描述一组数据变异程度或分散程度大小的指标。实际上，样本方差可以理解成是对所给总体方差的一个无偏估计。
。的使用称为贝塞尔校正（Bessel's correction），也用于样本协方差和样本标准偏差（方差平方根）。平方根是一个凹函数，因此引入负偏差（由Jensen不等式），这取决于分布，因此校正样本标准偏差（使用贝塞尔校正）有偏差。标准偏差的无偏估计是一个技术上涉及的问题，尽管对于使用术语的正态分布，形成无偏估计。无偏样本方差是函数
的U统计量，这意味着它是通过对群体的两个样本统计平均得到的。作为随机变量的函数，样本方差本身就是一个随机变量，研究其分布是很自然的。在
是来自正态分布的独立观察的情况下，Cochran定理表明s服从卡方分布：所以可求;和如果独立同分布，但不一定是正态分布，那么如果大数定律的条件对于平方观测值同样适用，则
是的一致估计量。可以看出，估计的方差趋于零。在Kenney and Keeping（1951：164），Rose和Smith（2002：264）和Weisstein（n.d.）中给出了渐近等效的公式。正态总体的样本均值和样本方差相互独立。
贾科莫·普契尼
Caroline Lufkin
翁建宇
Ivanov
玛丽亚·凯莉
仓野尾成美
遥控技术
CBD商务圈
公路改建工程
冰帽
核电设备